Probability of the complement of an event
Table of Content:
Probability of the complement of an event - Real Life Example
here is a table comparing the concept of an event and its complement in the context of a real-life example:
| Event | Complement |
|---|---|
| Being hired for a job | Not being hired for a job |
| Probability of being hired | Probability of not being hired |
| Increase in job skills and experience | Inadequate skills and experience |
| Health and well-being | Illness and injury |
| Exercise and healthy habits | Lack of exercise and unhealthy habits |
In each of these examples, the event represents a desired outcome or goal, and its complement represents the opposite or undesired outcome. The probability of the event occurring can be increased by taking steps to improve the relevant factors, such as job skills, health habits, or exercise routine. Conversely, the probability of the complement can be decreased by avoiding negative factors, such as unhealthy habits or lack of experience.
Formula :
The formula for the probability of the complement of an event is:
$$P(E^c) = 1 - P(E)$$
where \(E^c\) is the complement of the event \(E\). The complement of an event \(E\) is the set of all outcomes that are not in \(E\). The probability of the complement, denoted \(E^c\), is the probability that \(E\) does not occur. We can find the probability of the complement by subtracting the probability of \(E\) from 1, since the sum of the probabilities of \(E\) and \(E^c\) must equal 1.
Example 1:
Here is a table comparing the probability of an event and its complement:
| Event | Complement |
|---|---|
| \(E\) | \(E^c\) |
| \(P(E)\) | \(P(E^c) = 1 - P(E)\) |
| Rolling a 6 on a fair six-sided die | rolling a number that is not 6 |
As an example, let's consider the event of rolling a 6 on a fair six-sided die. The probability of this event is:
$$P(E) = \frac{1}{6}$$
The complement of this event is the event of rolling a number that is not 6, which has a probability of:
$$P(E^c) = 1 - P(E) = 1 - \frac{1}{6} = \frac{5}{6}$$
So the probability of rolling a number that is not 6 is greater than the probability of rolling a 6.
Example 2:
Let's say we have a fair six-sided die and we define the event \(E\) as rolling an odd number. Then the complement of \(E\) is the event of rolling an even number. The probability of the complement, denoted \(E^c\), is the probability of rolling an even number, which can be found using the formula:
$$P(E^c) = 1 - P(E)$$
where \(P(E)\) is the probability of rolling an odd number. Since there are three odd numbers and three even numbers on the die, we have:
$$P(E) = \frac{3}{6} = \frac{1}{2}$$
Therefore, the probability of rolling an even number (the complement of $E$) is:
$$P(E^c) = 1 - P(E) = 1 - \frac{1}{2} = \frac{1}{2}$$
So the probability of rolling an even number on the die is also \(\frac{1}{2}\).
Question:
Solution:
We can first calculate the probability of rolling doubles and then subtract that from 1 to find the probability of not rolling doubles.
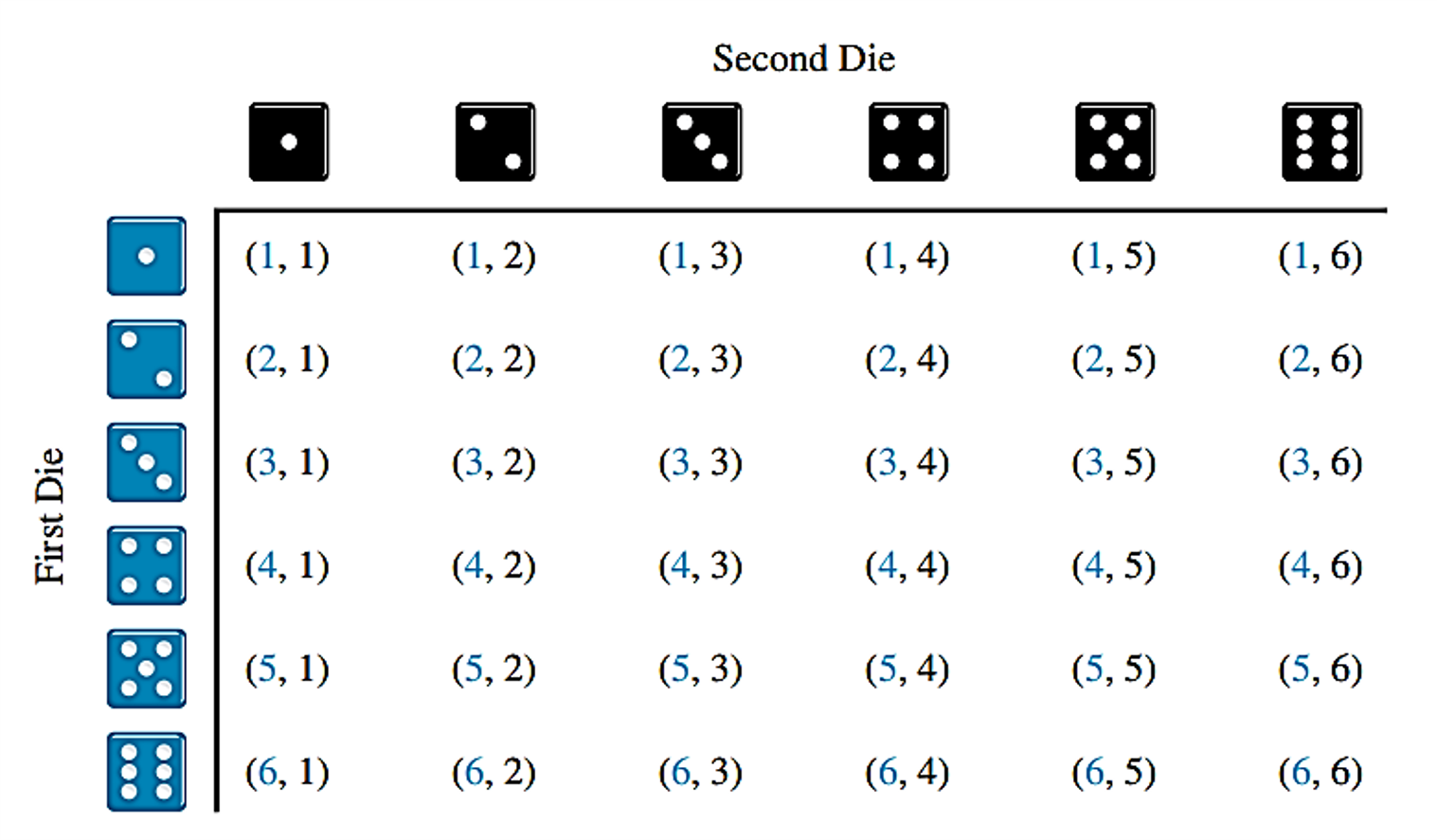
There are 6 possible outcomes when rolling a single die: 1, 2, 3, 4, 5, and 6. When rolling two dice, there are 6 x 6 = 36 possible outcomes.
Out of these 36 possible outcomes, there are 6 outcomes where doubles are rolled: (1,1), (2,2), (3,3), (4,4), (5,5), and (6,6).
Therefore, the probability of rolling doubles is 6/36 = 1/6.
$$P(E) = \frac{6}{36} = \frac{1}{6}$$The probability of not rolling doubles is the complement of rolling doubles, which is 1 - 1/6 = 5/6.
$$P(E^c) = 1 - P(E) = 1 - \frac{1}{6} = \frac{5}{6} = 0.8333$$So, the probability of not rolling doubles when rolling a pair of dice is \(\frac{5}{6}\) or approximately 0.8333.
Question:
A pair of dice are rolled. What is the probability of rolling 10 or less?
Solution:
To find the probability of rolling 10 or less with a pair of dice, we can use the fact that the complement of rolling 10 or less is rolling 11 or 12. Thus, we have:
\begin{align*} P(\text{10 or less}) &= 1 - P(\text{11 or 12}) \\ &= 1 - [P(\text{11}) + P(\text{12})] \\ &= 1 - \left(\frac{2}{36} + \frac{1}{36}\right) \\ &= \frac{33}{36} = \frac{11}{12} \end{align*}
Therefore, the probability of rolling 10 or less with a pair of dice is \(\frac{11}{12}\).
Question:
A gum ball machine contains gum balls of five different colors: 36 red, 44 white, 15 blue, 20 green, and 5 orange. The machine dispenser randomly selects one gum ball. What is the probability that the gum ball selected is:
a.) green?
b.) not green?
c.) not orange?
d.) orange?
e.) red, white, or blue?
f.) not a color in the flag of the USA?
Solution:
a) The probability of selecting a green gum ball is:
$$P(\text{green}) = \frac{\text{number of green gum balls}}{\text{total number of gum balls}} = \frac{20}{120} = \frac{1}{6}$$
b) The probability of selecting a gum ball that is not green is:
$$P(\text{not green}) = 1 - P(\text{green}) = 1 - \frac{1}{6} = \frac{5}{6}$$
c) The probability of selecting a gum ball that is not orange is:
$$P(\text{not orange}) = 1 - P(\text{orange}) = 1 - \frac{5}{120} = \frac{115}{120} = \frac{23}{24}$$
d) The probability of selecting an orange gum ball is:
$$P(\text{orange}) = \frac{\text{number of orange gum balls}}{\text{total number of gum balls}} = \frac{5}{120} = \frac{1}{24}$$
e) The probability of selecting a red, white, or blue gum ball is:
$$P(\text{red, white, or blue}) = \frac{36}{120} + \frac{44}{120} + \frac{15}{120} = \frac{95}{120} = \frac{19}{24}$$
f) The probability of selecting a gum ball that is not a color in the flag of the USA (red, white, or blue) is:
$$P(\text{not a color in the flag of the USA}) = 1 - P(\text{red, white, or blue}) = 1 - \frac{19}{24} = \frac{5}{24}$$